盛南燕
(浙江省新昌县育英小学 312500)
2015年11月县教研室举行了“空间与图形的研讨活动”,笔者有幸代表县骨干教师执教了“平移和旋转”一课,从教研员指定教学内容到登台上课的一个月半时间里,笔者经历了“平移和旋转”一课曲折的磨课过程,在一次次不厌其烦的设计、尝试、反思、重构中,感慨颇多。下面就主要详述在教学“计算平移的距离”这一环节中,我的所思所想。
从问题出发
几次听过这节课,教材中的第二个环节是“正确数出平移的格数”总是被老师们缩水成直接告知“要数出平移的距离只要看其中的一个点平移了几格”
师:小房子通过怎样平移能跟右边的小房子重合呢?要平移多少格呢?你能数出来吗?
生:向右平移1格
生:向右平移4格
师:同意1格的的举手,同意4格的举手,那我们来演示一下,到底谁说对了呢?(展示过程中对应点闪动)仔细看闪动的两个点,从这点到那点移了(3格),原来要知道一个物体平移了几格,只要找到其中一个点的对应点就可以了。
……
如此,“为什么只要数图形的其中一个点平移了几格”被跳过了,正确数出平移的格数也就演绎成了技能训练。在与老师的对话中,笔者也深切的感受到,许多老师也并没有去考虑过“为什么”,甚至没有意识到存在一个“为什么”。他们说:“告诉学生找到相应点一数,准没问题,如果一问为什么,他们倒不会算了……”。
真的是这样吗?
正确数出平移的距离,可以分解为二个层次,我们可以找到一个点以及它的对应点,并数出它们之间的距离。也可以找到一条线段以及它的对应线段,并数出它们之间的距离。教学思路可用以下图式来表示。
.png)
让学生在自主探索“怎样数物体平移的距离”,在教师的引导下进一步理解“为什么可以用数出相应点的距离来确定物体的移动距离”。这个过程使学生在个体认知背景下完成数学建模,这对于优化学生的认知结构,发展学生的认知策略,激发学生的研究兴趣,应该是有裨益的。
教学尝试一
考虑房子上的顶点较多,可能会对学生的学习造成负面影响,又根据低年级的年龄特点,笔者决定用“小鱼在格子图上移动找朋友”这一情境展开教学,尝试把“怎样求平移的距离”和“为什么可以这样求”的过程展开,但很快遇到了问题。
师:黄小鱼和红小鱼交朋友,它通过怎样平移能跟红小鱼重合呢?要平移多少格呢?
你能数出来吗?
.png)
生:向右平移1格(4格)。
师:到底是向右平移是1格还是4格?我们来互相辩论一下,1格的同学先来说说理由。
生:中间空了1格,
师:对呀!说平移4格的同学有意见了,你们来说说,
生:应该是4格,小鱼嘴巴是从这点平移到了那个点。(学生激动的跑上来指给大家看)
师:都同意4格了。
师:可我还是有疑问,为什么这个点移动了3格,黄小鱼就一定移动了4格,它的身子不是在后面吗?
生:小鱼身子也向前移动了4格。
师:我们也来数一下,也是4格,请大家在胆猜一下,黄小鱼的其他几个点会移动了几格?(学生猜)
师:我们就来验证一下。(故意将起点数成1)
生:错了,起点不能数1。
师:噢,我们在数的时候,起点只能数0,到后面的点才是移动了一格。
师:在数小鱼平移了多少格,我们还可以来数鱼身上的线段,我们一起来数一数。
生:1格,2格,3格,4格。
小结:小朋友真会观察,通过大家的发现我们知道了一个物体平移了几格,我们只要找其中一个点的对应点,再数出它们之间的距离。当然也可以找出其中的一条线段。
……
教学中通过教师的提议:“黄小鱼的其他几个点会平移了几格”学生正确数了其他点平移,以及线段平移的格子数。但从客观上说,由于教师的引导学生的操作成为了一种机械操练。如何从真正意义让学生明白物体平移的距离只要数出点移动的距离。
1、规律的得出仅仅是通过验证,够吗?
作为“平移距离”的教学,通过“猜想——验证——归纳”教学模式进行组织教学。一但物体的顶点不在表格的交点,学生很难正确数出物体平移的距离。可见学生对于为什么只要数出其中的一个点平移了多少格,只能说是“知其然”而“不知所以然”。因此,这一种教学模式作为“探究平移的距离”并不合适。
2、理解“平移距离”的支点在哪里?
同样是数格子教学,“平移距离”和一年级教学中“小动物爬几格能吃到相应的水果”有着诸多不同之处。从外在有形式来看,学生一年级学习中,已经正确数出小动物从这格爬到水果格子里一共要爬几格,学生对数格子已经有了比较丰富的感性认识。但在“平移和旋转”这节课中,是从一个点到相应点的距离,有着本质意义上的区别。寻找理解“平移距离”的支点,帮助学生建构完整的数学认识,显得尤为重要。经过思考,笔者认为学生对“点——线——面”的平移距离是学生把握“平移距离”的支点。
3、完整的认识“平移距离”有可能吗?
将平面图形的平移进行层层分解,先从点的平移开始,学生能轻易的判断点平移的距离,然后将许多个点汇集成线,数线平移的距离,这是一个从一维思维到二维思维的过程。最后由线组成平面图形,要正确数出平面图形平移的格数,自然学生就得出我们只要数出图形中点平移的距离,或者线平移的距离。通过这样层层分解,而后的层层深入,注重了从平移的本质层面上来理解,所以引导学生理解“平移的距离”也就变得容易了。
当学生在争论时,到底怎么来确定呢?是否可以从引领学生从点到线再到面有一个研究过程。
.png)
在自主的探究过程中,沟通点、线、面之间的联系,让学生感悟在求物体平移的距离为什么只要找出相应点平移的格子数,从而也渗透化繁为简的一种数学思考方法。基于这样的考虑,我进行了第二次尝试。
教学尝试二
师:黄小鱼想和红小鱼交朋友,它通过怎样平移才能跟红小鱼重合呢?要平移多少格呢?你能数出来吗?
.png)
生:向右平移1格(4格)
1、层层分解——由点到线
师:怎么来确定呢?我们可以先从简单的一个点来研究。(课件出示)
.png)
师:这红色小圆点平移到绿色小圆点那儿,要怎么平移呢?
学生:(异口同声)向右平移3格
师:可我觉得应该是4格。(教师故意将起点数成1)
生:老师你错了,起点上不能数1,因为还没移呢!
师:噢!原来如此,大家以后在数的时候可要注意啰!我们一起来数数,(数的过程课件中同步出现1、2、3数字)
.png)
师:红色小圆点要和黄色小圆点去交朋友,它又该怎么平移呢?(课件出示)
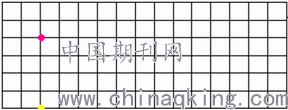
生:向下平移4格。
师:接下来我们来看线的平移。这线是由许许多多小圆点组成的。这红色有线要平移到绿线那儿,又该平移多少格呢?(课件出示)

生:向左平移2格
师:线向左平移了2格,那它上面的小圆点又怎么移动了呢?我们比一比谁的眼睛最亮,能发现其中的秘密!(课件演示:小圆点移动的过程)
生1:我发现小圆点向左平移了2格。
生2:线的平移时格数和线上面的点平移的格数是一样的。
师:你真是火眼金睛啊!我们在数线平移的时候只要数出线上的点平移的距离。线上的点平移了几格,线就平移了几格。
2、层层深入——由线到面
师:我们解决了点和线的平移,这种方法可不可以用到小鱼的平移上来呢?一起再来看看。到底黄小鱼要平移多少格呢?能告诉大家你是怎么想出来的?
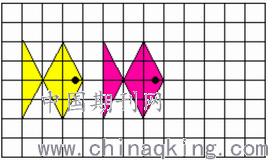
生1:4格。我是看小鱼嘴角的这个点到相应点平移了4格,小鱼就平移了4格
生2:我也是4格,不过我是数小鱼尾巴上那个点。
生3:我也是4格,我是数小鱼背上的这条线。
师:小朋友真会观察。通过大家的发现,我们知道了一个物体平移了多少格,我们只要找出其中的一个点或一条线,再看平移后相应点的位置,数出中间的格子数就可以了。
3、步步为营——优化策略
师:那老师数小鱼身上这个点可以吗?(这个点不在格子图的交点上)
学生思考了片刻。
生1:可以的,
师:你是怎数出来的呀?
生:(学生跑上来)这个点相应点在这儿,从那处点到这个点就是平移了3格。
生2:我也觉得可以,不过好像有点麻烦。
师:他们说的有道理吗?是啊,我们可去数物体上的任意一个点或者任意一条线,不过,我们一定选择容易找的这些点,这样才不容易出错!
……
我的反思
1、认知理解的过程是学生构建“知识链”的过程
学生对于为什么可以用数点方法来数物体平移的格数,通过层层分解又通过层层深入,让学生从真正意义上理解知识的内涵。学生有了“点的平移”作为学习的支点,再结合多媒体的直观演示从“一个点平移到另一个点”,又通过教师错误的数法,让学生纠错的过程,学生很清晰地把握了“平移距离”的本质,又有“线的平移”作为学习的阶梯,学习面的平移就水到渠成了。而正是这样的一个学习过程,学生沟通了知识间的联系,建构起了完整的“知识链”,使其原有知识结构中模糊的经验发展成了“科学的结论”。
2、认知理解的过程是学生数学思维提升的过程
突出数学学习过程的思考性,让学生在学习过程中思维始终处于活跃的状态,这是一节成功数学课的重要特征。在层层分解中,在矛盾中将复杂的问题简单化,从点的平移的研究到线的平移,到层层深入再到步步为营,三个层次的学习始终体现出浓浓的数学思考的味道。
第一层次:当学生争执不定时,教师提出:“怎么来确定呢?我们先简单的来研究一下。”这一问题,引导学生用“化难为易”的方法来解决问题,促使学生的思维从关注当前面的学习材料到数学系统中去思考,寻找新知建构的支点。这一环节是学生的思维从具体上升到抽象的过程,同时也是引导学生进入到数学层面思考的基础。
第二层次:解决了点和线的平移距离,教师通过:“我们解决了点和线的平移,这种方法是否可以用到小鱼上来的?”这一问题,又一次将学生的思维引向深处,教师通过:“小鱼到底平移了多少格呢?能告诉大家你是怎么想的?”这一问题,引发学生的再思考,然后向大家展示了不同的数法,体现了算法的多样化,学生的思维水平上升到了理解层面上。
第三层次:课进行到学生能用多种方法正确解决问题时,笔者并没有停止继续深入教学,进而质疑“数鱼身子和的点尾巴这个交点可以吗可以吗?”又一次将学生的思维引向高潮。学生自觉认定方法是可以的,可是会很麻烦,这时教师的目的也就水到渠成了,学生明白了,这些点移动的格子数是一样的,但是我们要选择容易找的点,自然进行了算法的优化。
在教学中,三个层次的学习,让学生自然而然地进入到思维的进程中,无痕迹的提升思维水平,引导学生内化知识,学生的数学思维已经从被动引向了自觉,不知不觉中学生还收获了“化难为易”的解决问题的方法,这一环节较好的阐释了数学建模过程——层层分解的策略。保证了学生有充分时间和空间参与建模的全过程,也让我们的教学更有效!