摘要:本文基于傅里叶热传导定理,运用有限差分方法,建立了高温防护服的热传导模型。考虑人体的散热机制,假设再防护服四层与人体热源之间还有第五层,采用粒子群算法对第五层参数进行标定。对于最有厚度的设计,建立有关生产成与厚度评价体系。
1.数据来源与创新点
本文数据主要来源于 2018 年全国大学生数学建模竞赛主办方提供。本文在皮肤外侧温度及服装厚度等参数确定的情况下,提出第Ⅴ层,即:人体内层。从而使得到的模型解更贴近于实际值。
2. 显格式差分方法建立热传导偏微分方程的数值求解
2.1 研究思路
未使用的服装在室内的温度大致和正常室温相同,假人穿着专用服装进入高温环境中的初始温度已定,即外界温度、中间温度 Ⅰ~ Ⅴ层和内层温度都已确定;其次,以距离为x轴,以时间为 y轴,以温度为z轴,建立空间坐标系.在坐标系下,将距离和时间划分为若干层,建立和时间、位置有关的热传导函数模型,由显式差分法,求解下一时刻不同位置的温度;最后,其它时刻对应的温度以此类推,即可求出外侧温度的变化情况。
2.2 热传导模型的建立
设人体温度分布函数, 依据导热学中的傅里叶实验定律可得
.png)
其中,k为物体的热传导系数,取正值。
在本文的研究内容中,已知在同一层的物体材料下的、和为定值,因此同一层的物体可以看作是均匀的,此时、及均为常数(不同层间的值不相同),记 ,得,
.png)
(3)
即为一维热传导方程。
分离变量求解边界条件
利用分离变量的方法求解边界条件,已知函数是关于变量、的函数
.png)
⑸
其中,为正常数。
由分离变量法求解,令
.png)
⑹
其中, 表示仅与有关的函数;
表示仅与t有关的函数。
将⑹带入方程,可得到,
.png)
⑺
即

把代入以上方程中得,

⒀
其中, 是在位置变系数有关的位置温度函数;
是在时间、变系数有关的瞬时温度函数;
是温度函数在初始零时刻的初始温度函数;
为仅考虑位置的温度函数。
将连续变化的空间和时间离散化,建立离散模型的坐标系、列写显格式差分方程,确定傅里叶系数,用离散点的温度数值解代替连续的温度函数.
3. 最优厚度设计
3.1 问题一
当环境温度为 65oC、IV 层的厚度为 5.5 mm 时,确保工作 60 分钟,假人皮肤外侧温度不超过 47oC,且超过 44oC 的时间不超过 5 分钟,确定 II 层的最优厚度。
对于模型一的建立,针对当前问题,防护服装在能达到防护作用情况下,厚度越薄越好,确定 II 层的最优厚度为目标函数,目标搜索空间为一维。
设立有N 个粒子组成一个群体,其中第个粒子位置表示为 ,即是第个粒子在一维搜索空间的位置.则以表示第二层的厚度。然后,把问题二的条件代入上述的差分模型计算,得到最高温度及超过所限定温度的持续时间。
把假人外侧温度条件和工作时间定为约束条件,则求解适应值具体流程如下
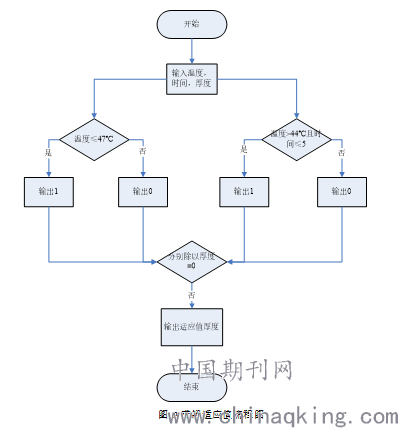
则对于该问题中,第II 层的厚度范围是,本文以1mm 定位为空气层 速度,4mm 定为第II 层速度,以1s 为更新时间。因此,每次粒子更新有位移和速度约束在范围[4,4]中。粒子的位置会不断地更新,直到迭代终止。最终筛选出的最优适应值即为目标函数要求的最优厚度。
最终求解得到:目标函数x(第II 层厚度)为,符合问题二对第II层的厚度要求。
3.2 问题二
当环境温度为时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过,且超过的时间不超过5分钟。
针对当前问题,需要求解第II 层和第IV 层的最优厚度。建立模型二,在模型一的基础上,把目标函数设为服装质量,目标搜索空间改为二维,其它约束条件不变, 通过对服装重量的优化求解,调用模型二的粒子群优化模型对目标函数进行优化求解,得到两个层厚度的最优设计。
首先,第II层和第IV层的厚度是未知量,分别设为。而其它层的厚度、各层的密度均为已知值.其次,令各层的重量为,各层的密度为,服装总质量为。则目标函数为
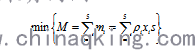
⒁
其中为包围曲面面积,。
最终求解得到:两个层的最优厚度,即。
3.3对于问题二模型优化
由于模型二中求解得到空气层的厚度,不太符合实际情况,现在假设空气层的厚度已知,以此求解第II 层的厚度.
我们给出确定的10组有等差关系的空气层厚度,代入为一维搜索空间的模型二中得到第II 层的厚度,所得如表1。

4. 结语
本文在皮肤外侧温度及服装厚度等参数确定的情况下,首先结合热传导学的理论知识,建立热传导模型。根据傅里叶实验定律建立热传导方程,并通过显格式差分方法建立热传导偏微分方程的数值求解算法,最后根据已知条件得出各层温度变化数据。利用粒子群算法,设定目标函数,得出最优的设计厚度。
参考文献
[1]]姜启源 谢金星 叶俊.数学模型.4 版.北京:高等教育出社,2011
[2]谷超豪 李大潜 陈恕行 郑宋穆 谭勇基 数学物理方程 第二版高等教育出版社 2002.7
[3]陈光亭 裘哲勇 数学建模.2 版.北京.高等教育出版社,2014
[4]卓金武 MATALAB 在数学建模中的应用.北京.北京航空航天大学出版社,2011